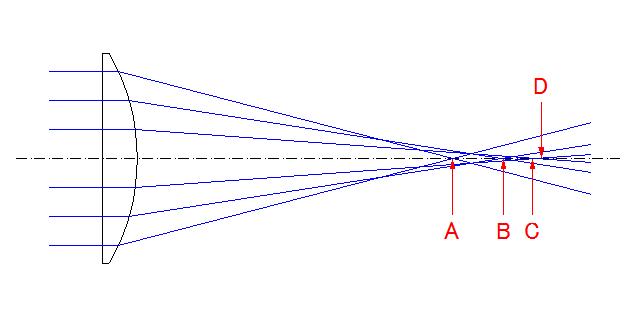
それぞれ光学系の光線の集光の様子を正確に描いたのが下図です。まず、説明を始める前にお断りがあります。光学業界では光学系の光路図を描いた場合、「光は左から右へ進む」約束がありますので、光線群は左側から出てレンズを通過し、右側に「結像」することになります。
　さて、右側の集光状態のまとまりが良ければ「良い結像（収差が小さい）」であり、散らばっていれば「悪い結像（収差が大きい）」になります。下図をよく見て比べてください。
　　　　　　　　　　　
�@平凸レンズ平面側を合わせた場合の集光状態
　　　　　　　　　
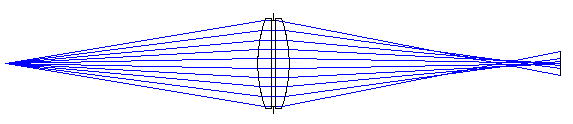
�A平凸レンズの球面側を合わせた場合の集光状態
　　　　　　　　　

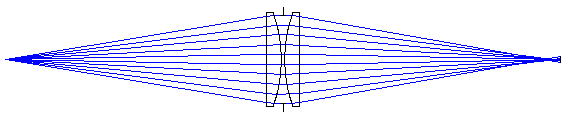
�B両凸レンズ２枚で構成した場合の集光状態
　　　　　　　　　
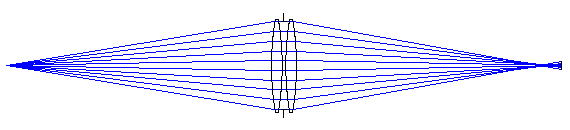
これらを見ると、�Aと�Bは�@と比べて格段に良い結像をしています。�Aと�Bも共に良い結像ですが、わずかに�Aが優っています。
また、�@と�Aを比べると大切なことがわかります。つまり、同じレンズを購入しても、その並べ方次第で結像結果には大きな違いが出ることを示しているので注意が必要です。
　さて、どうしてこのような結果になるのでしょうか？その違いは、レンズの屈折面が光線を曲げる「回数」です。
2枚のレンズ間での光束はほとんど平行になっていますが、�@の場合は、この区間でレンズ面が平面であるため実質上屈折作用がありません。
　これに比べて�Aの場合は、４面ある屈折面でそれぞれ少しづつ屈折作用をさせていることがわかります。また、�Bも�Aと同じことが言えます。つまり「光線は少しづつ曲げること」が「収差を良くする条件」なのです。

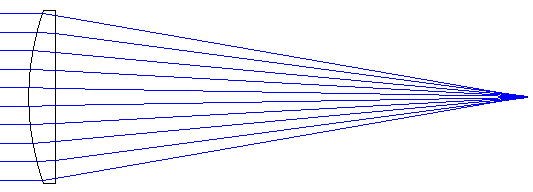
　さてここで、少し寄り道をします。�Bも�Aと同レベルなのですが平凸レンズの組合せが両凸レンズの組合せに比べてなぜより優位なのかを考察します。さて、下に示す上２つの光路図を見てください。

＜平凸レンズ＞
　　　　　　　　

＜ベストフォームレンズ＞
　　　　　　　　

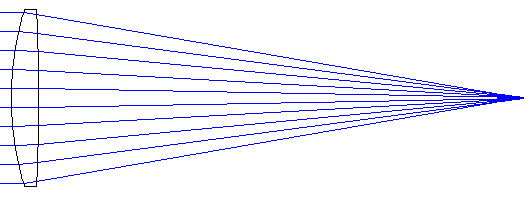
お互いにとてもよく似ていますが、上側は今回考えている平凸レンズの、下側は「ベストフォームレンズ」と呼ばれるレンズの集光状態を示しています。「ベストフォームレンズ」とは、平行光束に対して単レンズとしては最良の結像（軸上での）をするレンズのことで、レンズの右側が平面ではなく僅かに曲率を持ったレンズになっています。本図では集光状態の差はほとんど見分けがつかなくなっていますが、今後解説する予定の「収差図」を見ると「ベストフォームレンズ」が僅かに優秀なレンズになっています。

　にもかかわらず平凸レンズが実験等ではよく使われる理由は、軸上での収差がベストフォームレンズと同じぐらい少なく、しかも製造上作りやすく安価であるからです。
　また、両凸レンズ単体についても次に示します。この図から上の２つのレンズと比べて少し性能が劣っていることがわかります。
　　　　　　


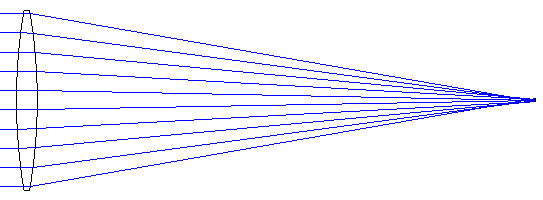
　ところで、�Aよりももっと良い結像しているのが下図です。これは、「ダブレットレンズ（アクロマートレンズ）」を2枚組み合わせたもので、屈折面が６面あることでさらに良い結像になっています（平凸レンズよりも高価です）。
もちろん、この場合でもレンズの向きに気をつけてください。平行光束になっている側でもしっかり屈折作用をさせるように、曲率半径のきつい方をより平行光束に近い方に向けることが条件です。
　　　　　　

　　　　

学校で学んだ「焦点の位置」は平行な光線がレンズを通過後光軸と交わるところ、でしたが、実在するレンズでは大なり小なり上図のように色々な場所で交差してします（球面収差があるといいます）。こうなると「焦点位置」は色々なところにあることになってしまいますが、実は焦点位置は、

　　　　　　　　　　「光軸に非常に近いすれすれの光線（近軸光線と言います）がレンズ通過後光軸と交わる位置」

と「定義」されているのです。従ってこの平凸レンズの焦点位置は、「A」〜「C」ではなく実は「D」になります。

　上記レンズの場合、レンズの屈折率を「n」後ろ側の曲率半径を「r（この場合符号はマイナスになります）」とすると、後ろ側の球面の面頂から焦点までの距離「BFD」（バックフォーカスと言います）は、次式で与えられます。この位置が「焦点の位置」です。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　
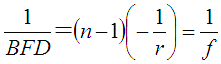
　また、この向きの平凸レンズの場合、バックフォーカスは「焦点距離：f」にも等しくなります。

　屈折率を定性的に言えば、界面における光線の屈折の程度を左右する係数、と言えると思いますが、物理的には次式で定義されます。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
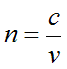
　ここで、「c」は真空中の光速、「ν」はその物質中の光速です。つまり、「真空中の光速と物質中の光速の比」になります。一般に物質中の光速は真空中のそれと比べて小さくなりますので屈折率は常に「１」よりも大きくなります。
　この屈折率は、波長によっても変化します。下図は、「ＢＫ７」と呼ばれる光学ガラスについて屈折率と波長の関係を示したもので、一般に波長が短くなると屈折率は大きくなります。そして、ガラス材料の種類によって屈折率の値やその波長に対する変化の様子は異なっています。
　　　　　　　　　　　　　　　　　　
レンズに使われるガラスは「光学ガラス」と呼ばれ、いろいろな種類（屈折率：およそ1.45〜2まで）のガラスが用意されており、それらは厳密に屈折率が制御されて市販されています。その精度は、通常「n=±0.0005」、特注では「n=±0.0002」までの制御がなされています（株式会社　オハラのカタログより）。同時に、「脈理（屈折率のゆらぎ）」の少ないガラスであることも「光学ガラス」の条件になります。
これらのガラスをうまく組み合わせることで収差の少ないレンズが構成され、しかもいつ作っても同等な性能を安定して維持できることになります。

　まず、第１面に法線を立てます。この場合、球面ですから下図のように第１面の曲率中心から引いた線がそのまま法線になります。この入射角と屈折率を使いスネルの法則からレンズ内に入る屈折角が計算できます。次に、この光線が第２面と交差する点で法線を立てます。これも第１面同様、第２面の曲率中心を結ぶ直線が法線になります。そして、このときの入射角度を求め、同様にスネルの法則を適用します。このように作図をすると下図の赤色線で示した光路が求められます。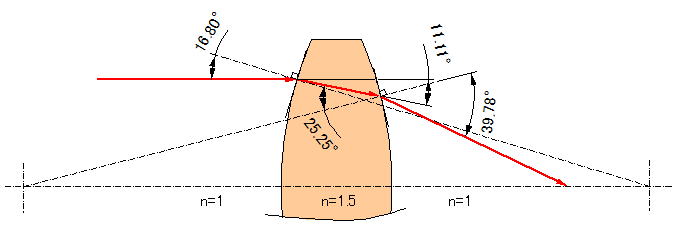
　さて、パソコンが普及した現在では、こうした光線追跡は光学設計ソフトが簡単に行なってくれます。以下に同じ条件結果を示します。結果は瞬時に得られます。
　　　　　　　　　　　　　　　

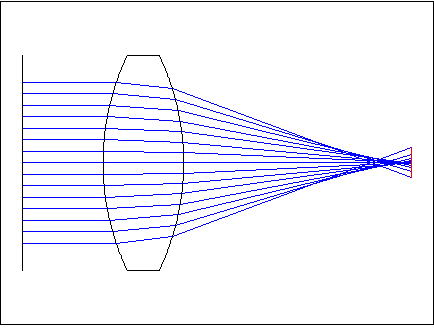
　問いの図から全反射が起こるときは、屈折角が90度になります。これをスネルの法則に代入します。ここで、この図から今回は入射側の屈折率がn₂で、出射側の屈折率がｎ₁になります。このときは、屈折角が90°になりますので次式が得られます。
　　　　　　　　　　　　　　　　　　　　　　　　　
つまり、
　　　　　　　　　　　　　　　　　　　　　　　　　　
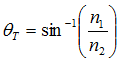
　ここで、「θ_T」は全反射（Total reflection）を起こすときの入射角です。この角度を「臨界角」と言います。

　さて、ここで注意することがあります。この全反射が起こるときは必ず「屈折率の高い物質から低い方へ入射するときのみ起こる」ということです。つまり屈折率が低い方から入射する場合はありえないということです。
　このことは、当然ですが上式を見てもわかります。sinは「１」より小さいことから、次の式が成立します。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
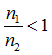
従って、　　　　　　　　　　　　　　　　　　　　　　　　
　つまり、入射側の屈折率は出射側のそれに比べて必ず高くなります 。

　一般に光線が屈折率n₁の物質から屈折率n₂の物質に垂直入射する場合、その「表面反射率：R_ref」は次式で与えられます。
　　　　　　　　　　　　　　　　　　　　　　　　　　　

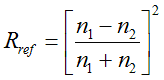
この式を使って各物質の表面反射率を計算すると次のようになります。
　　　　　　　　
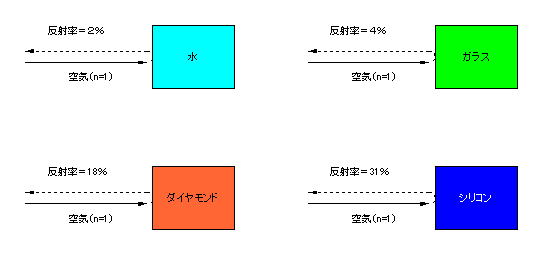
　これを見ると、ガラスは１面当たり約４％の反射があることがわかります。また、ダイヤモンドは通常のガラスと比べて非常に高く、よく反射して見えることがわかります。さらに、上式からわかるように、この表面反射率は屈折率の関数になっていますが、従って波長によっても反射率が異なることがわかります。

　ところで、実はこの反射率は「入射する光線の角度」によっても大きく異なります。シリコンの場合を見てみましょう。下図は横軸に入射角度、縦軸に反射率を取ったグラフです。ここで、青色 の曲線は「S偏光」と呼ばれる入射面に垂直な偏光成分の反射率、緑色の曲線は「P偏光」と呼ばれる入射面に平行な偏光成分の反射率を、赤色の曲線は２つ偏光成分の平均反射率を示しています。
　入射角度が０度場合、反射率は約31％です。ところが「S偏光」は入射角が大きくなるにしたがって反射率が高くなり、一方「P偏光」は逆に反射率が減少しある角度でゼロとなり、それから大きくなって行きます。このように、反射率は偏光成分によって大きな変動を示すのです。
　　　　　　　　　　　　　　

　ところで、上図のように「P偏光」の反射率はある角度でゼロになりますが、この角度をその研究者の名前から「ブリュ−スター(Brewster)角」と呼びます。それは次式で与えられます。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　
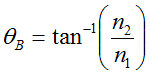
　　　　　　　　　　　　　（この式にn₁＝1、n₂＝3.5を代入するとθ_B=74°になります。）

この現象を使う非偏光な光束を直線偏光だけにすることができます。

　答えは「C」です。実例を示した下図に示すように、一般に物質の屈折率は波長が短くなると大きくなります。しかも、その程度は物質によって異なっていて、その物質固有の特性を示します。従って、一口に「屈折率」といっても、「どの波長に対する屈折率」かを指定しなければならないことがわかります。
　　　　

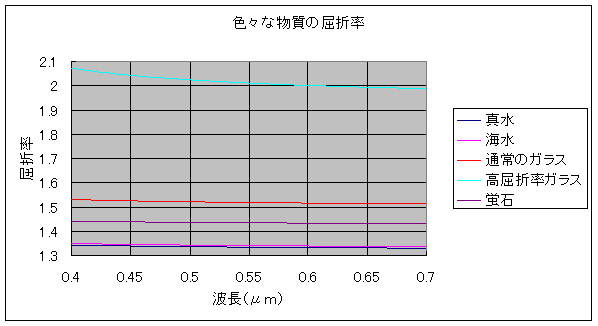
それでは、個々の物質について詳細に見ていきます。

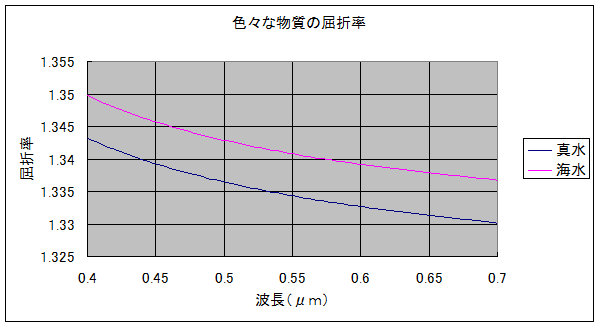
・真水と海水の比較
　真水と海水では海水の方が屈折率が高いことがわかります。具体的には、波長500nm付近でその差は「0.0064」程度あることがわかります。
　　　　

・光学で使われるガラス類の比較
　レンズ等光学部品に使われる材料を比較してみます。ここで、「通常のガラス」は最もポピュラーな光学ガラス「ＢＫ７」のことです。光学設計では色々な特性をもつ光学材料を使用して目的とする光学性能のより良い（一般的には収差の少ない）レンズを追求しますが、このとき使用する光学材料の種類は例えば「ＢＫ7」というようにアルファベットと数字を組み合わせた記号で表示されます。これはガラス材料供給メーカーによって異なり、それぞれ固有の記号になります。「BK7」の屈折率はこの波長範囲で1.5より少し大きな値になっています。
　次は「高屈折率ガラス（材料記号：S-LAH79）」です。屈折率はほぼ「２」になっていますが、「ＢＫ７」と比べて短波長側でより屈折率が大きくなる特徴（曲線が跳ね上がる）を持っています。一般に波長が異なると屈折率が変わる現象を「分散」と言いますが、この場合「S-LAH79」は「BK7」より分散の大きな材料、ということになります。
　　　　　　

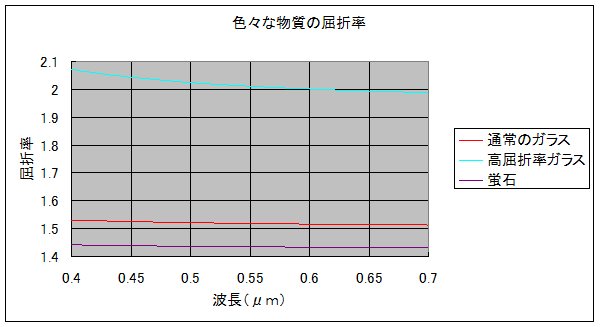
　さて、「蛍石」は通常のレンズ材料（ガラス＝アモルファス状）」では無く「結晶」です。この材料は特に天文観望ファンには垂涎の光学材料です。この材料で作ったレンズを組み込むと焦点距離の長い天体望遠鏡でも色収差の非常に小さい、色にじみの少ない像が得られるからです。「蛍石」は（上図では少しわかりづらいですが）、通常のガラス材料と比べて短波長に行っても屈折率があまり上がらない「異常に小さな分散特性」を持っています。
　また、この「蛍石」に近い特性を持った光学ガラスも販売されていて、例えば「S-FPL53やS-FPL51(オハラガラス)」や「FCD1(HOYAガラス)」があり、「異常分散ガラス」あるいは「ED（Extra low Dispersion）ガラス」と呼ばれていて写真レンズのカタログにも載っています。